Nacho Abeledo, Ramón Abeledo, Abeleh

Nacho Abeledo: Ignacio "Nacho" de Loyola Abeledo Rute est un footballeur espagnol qui joue pour le CD San ​​Roque de Lepe en tant qu'ailier gauche.
Ramón Abeledo: Ramón Gregorio Abeledo est un milieu de terrain argentin qui a joué pour l'Argentine lors de la Coupe du Monde de la FIFA 1962. Il a également joué pour le Club Atlético Independiente.
Abeleh: Abeleh peut faire référence à: Ableh (homonymie) Abeleh, Khuzestan
Abeleh, Khuzestan: Abeleh est un village du district rural de Rud Zard, dans le district central du comté de Bagh-e Malek, dans la province du Khuzestan, en Iran. Lors du recensement de 2006, son existence a été notée, mais sa population n'a pas été déclarée.
Ableh-ye Sofla: Ableh-ye Sofla est un village du district rural de Holayjan, dans le district central du comté d'Izeh, dans la province du Khuzestan, en Iran. Lors du recensement de 2006, sa population était de 215 habitants, répartis dans 38 familles.
Ableh-ye Sofla: Ableh-ye Sofla est un village du district rural de Holayjan, dans le district central du comté d'Izeh, dans la province du Khuzestan, en Iran. Lors du recensement de 2006, sa population était de 215 habitants, répartis dans 38 familles.
Manfred Abelein: Manfred Abelein était un homme politique allemand. Il était un représentant de l'Union chrétienne-démocrate allemande.
Abelemkpe: Abelenkpe est une zone urbaine du district métropolitain d'Accra, un district de la région du Grand Accra au Ghana.
Langue abellen: Abellen , Abenlen , Aburlin ou Ayta Abellen , est une langue sambalique. Il compte environ 3500 locuteurs et est parlé dans quelques communautés Aeta de la province de Tarlac, Philippines Ayta Abellen elle-même fait partie de la famille des langues sambaliques aux Philippines et est étroitement liée non seulement aux 5 autres dialectes Ayta, mais aussi au dialecte botolan de Sambal.
Langue abellen: Abellen , Abenlen , Aburlin ou Ayta Abellen , est une langue sambalique. Il compte environ 3500 locuteurs et est parlé dans quelques communautés Aeta de la province de Tarlac, Philippines Ayta Abellen elle-même fait partie de la famille des langues sambaliques aux Philippines et est étroitement liée non seulement aux 5 autres dialectes Ayta, mais aussi au dialecte botolan de Sambal.
Langue abellen: Abellen , Abenlen , Aburlin ou Ayta Abellen , est une langue sambalique. Il compte environ 3500 locuteurs et est parlé dans quelques communautés Aeta de la province de Tarlac, Philippines Ayta Abellen elle-même fait partie de la famille des langues sambaliques aux Philippines et est étroitement liée non seulement aux 5 autres dialectes Ayta, mais aussi au dialecte botolan de Sambal.
Langue abellen: Abellen , Abenlen , Aburlin ou Ayta Abellen , est une langue sambalique. Il compte environ 3500 locuteurs et est parlé dans quelques communautés Aeta de la province de Tarlac, Philippines Ayta Abellen elle-même fait partie de la famille des langues sambaliques aux Philippines et est étroitement liée non seulement aux 5 autres dialectes Ayta, mais aussi au dialecte botolan de Sambal.
Leonardo Abelenda: Leonardo Daniel Abelenda Rodríguez est un footballeur uruguayen qui joue actuellement pour la Plaza Colonia dans la Segunda División uruguayenne.
Leonardo Abelenda: Leonardo Daniel Abelenda Rodríguez est un footballeur uruguayen qui joue actuellement pour la Plaza Colonia dans la Segunda División uruguayenne.
Abelemkpe: Abelenkpe est une zone urbaine du district métropolitain d'Accra, un district de la région du Grand Accra au Ghana.
Jim Abeler: James J. Abeler II est un politicien du Minnesota et membre du Sénat du Minnesota. Membre du Parti républicain du Minnesota, il représente le district 35 de la région métropolitaine des villes jumelles du nord. Il représentait auparavant le district 35A à la Chambre des représentants du Minnesota.
Jim Abeler: James J. Abeler II est un politicien du Minnesota et membre du Sénat du Minnesota. Membre du Parti républicain du Minnesota, il représente le district 35 de la région métropolitaine des villes jumelles du nord. Il représentait auparavant le district 35A à la Chambre des représentants du Minnesota.
Abeles: Abeles est un nom de famille anglais et juif, dérivé du nom biblique Abel. Les personnes notables avec le nom de famille comprennent: Benjamin Abeles, physicien américain Edward Abeles (1869-1919), acteur américain Florin Abelès (1922-2005), physicien français John H Abeles, homme d'affaires américain Kim Victoria Abeles, artiste américaine Michele Abeles, artiste américaine Peter Abeles (1924–1999), homme d'affaires australien Moshe Abeles, chercheur israélien sur le cerveau Norman Abeles, psychologue américain d'origine autrichienne Ruth Abeles, gymnaste olympique israélienne Sigmund Abeles, artiste figuratif américain
Benjamin Abeles: Benjamin Abeles était un physicien austro-tchèque dont les recherches dans les années 1960 aux États-Unis sur les alliages de germanium-silicium ont conduit à la technologie utilisée pour alimenter des sondes spatiales telles que le vaisseau spatial Voyager . Il a grandi en Autriche et en Tchécoslovaquie et est arrivé au Royaume-Uni en 1939 pour l'une des missions de Kindertransport . Il a terminé ses études après la guerre en Tchécoslovaquie et en Israël, obtenant un doctorat en physique. Il a ensuite vécu et travaillé comme physicien de recherche aux États-Unis et a pris sa retraite en 1995. Ses honneurs comprennent la médaille Stuart Ballantine de 1979 et son intronisation au New Jersey Inventors Hall of Fame (1991).
Peter Abeles: Sir Peter Emil Herbert Abeles , AC était un magnat australien des transports. Réfugié de Hongrie, il est devenu homme d'affaires en Australie et a été fait chevalier en 1972.
Méthode de la matrice de transfert (optique): La méthode de la matrice de transfert est une méthode utilisée en optique et en acoustique pour analyser la propagation des ondes électromagnétiques ou acoustiques à travers un milieu stratifié. Ceci est par exemple pertinent pour la conception de revêtements antireflets et de miroirs diélectriques.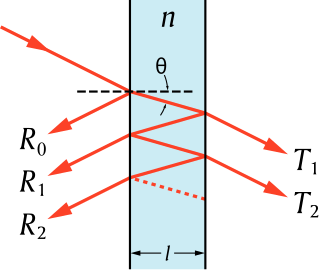
Abalessa: Abalessa est une ville et une commune de la province de Tamanrasset, dans le sud de l'Algérie, coextensive avec le district du même nom. Selon le recensement de 2008, elle compte 9 163 habitants contre 6 484 en 1998, avec un taux de croissance annuel de 3,6%. Abalessa est située le long de l'ancienne route commerciale transsaharienne, à 80 kilomètres à l'ouest de la ville de Tamanrasset, la capitale de la province. Le code postal de la ville est 11120.
Abalessa: Abalessa est une ville et une commune de la province de Tamanrasset, dans le sud de l'Algérie, coextensive avec le district du même nom. Selon le recensement de 2008, elle compte 9 163 habitants contre 6 484 en 1998, avec un taux de croissance annuel de 3,6%. Abalessa est située le long de l'ancienne route commerciale transsaharienne, à 80 kilomètres à l'ouest de la ville de Tamanrasset, la capitale de la province. Le code postal de la ville est 11120.
Johann Philipp Abelin: Johann Philipp Abelin était un chroniqueur allemand dont la carrière chevauchait les XVIe et XVIIe siècles. Il est né, probablement, à Strasbourg, et y mourut entre 1634 et 1637. Il écrivit de nombreuses histoires sous les pseudonymes d' Abeleus , Philipp Arlanibäus , Johann Ludwig Gottfried et Gotofredus .
Oxytrigona tataira: Oxytrigona tataira , communément appelée tataíra ou abelha-de-fogo , est une espèce d'abeille eusociale sans dard de la famille des Apidae et de la tribu Meliponini.
Abelhaleem Hasan Abdelraziq Ashqar: Abelhaleem Hasan Abdelraziq Ashqar est un activiste musulman palestinien qui a été brièvement professeur adjoint de commerce à l'Université Howard. Il a été reconnu coupable d'outrage et d'entrave à la justice pour refus de témoigner devant un grand jury dans un procès lié au financement du Hamas par des donateurs aux États-Unis, et a été condamné en novembre 2007 à 135 mois de prison.
Abelhaleem Hasan Abdelraziq Ashqar: Abelhaleem Hasan Abdelraziq Ashqar est un activiste musulman palestinien qui a été brièvement professeur adjoint de commerce à l'Université Howard. Il a été reconnu coupable d'outrage et d'entrave à la justice pour refus de témoigner devant un grand jury dans un procès lié au financement du Hamas par des donateurs aux États-Unis, et a été condamné en novembre 2007 à 135 mois de prison.
Abelheira: Abelheira est un village de la municipalité de Lourinhã au Portugal.
Paroisse de Ābeļi: La paroisse de Ābeļi est une unité administrative de la municipalité de Jēkabpils, en Lettonie.
Paroisse de Ābeļi: La paroisse de Ābeļi est une unité administrative de la municipalité de Jēkabpils, en Lettonie.
Abelia: Abelia est un genre autrefois reconnu qui contenait environ 30 espèces et hybrides, placés dans la famille des chèvrefeuilles, Caprifoliaceae. Des études de phylogénétique moléculaire ont montré que le genre n'était pas monophylétique, et en 2013, Maarten Christenhusz a proposé la fusion d' Abelia dans Linnaea , avec d'autres genres. Section Abelia Zabelia a été élevée au genre Zabelia .
Abelia (organisation): Abelia est une organisation d'employeurs en Norvège, organisée dans le cadre de la Confédération nationale des entreprises norvégiennes.
Abelia (organisation): Abelia est une organisation d'employeurs en Norvège, organisée dans le cadre de la Confédération nationale des entreprises norvégiennes.
Linnaea chinensis: Linnaea chinensis , synonymes Abelia chinensis et Abelia rupestris , est une espèce de plante à fleurs de la famille des chèvrefeuilles Caprifoliaceae. Il a été décrit par Robert Brown en 1818 et transféré au genre Linnaea en 1872, bien que ce mouvement n'ait pas été largement accepté avant 2013. La plante habite la Chine, Taiwan et le Japon. C'est un arbuste caduc compact avec des tiges rougeâtres et de petites feuilles brillantes qui deviennent brun rougeâtre avant l'automne. C'est l'une des espèces les plus résistantes au froid du genre.
Linnaea chinensis: Linnaea chinensis , synonymes Abelia chinensis et Abelia rupestris , est une espèce de plante à fleurs de la famille des chèvrefeuilles Caprifoliaceae. Il a été décrit par Robert Brown en 1818 et transféré au genre Linnaea en 1872, bien que ce mouvement n'ait pas été largement accepté avant 2013. La plante habite la Chine, Taiwan et le Japon. C'est un arbuste caduc compact avec des tiges rougeâtres et de petites feuilles brillantes qui deviennent brun rougeâtre avant l'automne. C'est l'une des espèces les plus résistantes au froid du genre.
Linnaea chinensis: Linnaea chinensis , synonymes Abelia chinensis et Abelia rupestris , est une espèce de plante à fleurs de la famille des chèvrefeuilles Caprifoliaceae. Il a été décrit par Robert Brown en 1818 et transféré au genre Linnaea en 1872, bien que ce mouvement n'ait pas été largement accepté avant 2013. La plante habite la Chine, Taiwan et le Japon. C'est un arbuste caduc compact avec des tiges rougeâtres et de petites feuilles brillantes qui deviennent brun rougeâtre avant l'automne. C'est l'une des espèces les plus résistantes au froid du genre.
Église Abelia: L' église Abelia de la Trinité est une église orthodoxe géorgienne du XIIIe siècle, située dans la municipalité de Tetri Tsqaro, dans la région du centre-sud de la Géorgie, Kvemo Kartli. De conception simple à nef unique, il est situé à la périphérie du village moderne d'Abeliani, anciennement connu sous le nom d'Abelia. Une référence à la diarchie en Géorgie sous la domination mongole dans une inscription sur le mur sud de l'église permet de dater la construction à la période 1250-1259. L'église est inscrite sur la liste des monuments culturels immobiliers d'importance nationale de Géorgie.
Zabelia corymbosa: Zabelia corymbosa est une espèce de plante à fleurs de la famille des chèvrefeuilles, Caprifoliaceae. Il est originaire d'Asie centrale, où il se trouve au Kazakhstan, au Kirghizistan et au Tadjikistan.
Linnaea spathulata: Linnaea spathulata , synonyme Abelia spathulata , est une espèce de Linnaea de la famille des chèvrefeuilles (Caprifoliaceae). La plante est endémique de Corée et du Japon.
Linnaea floribunda: Linnaea floribunda est une espèce de plante à fleurs de la famille des chèvrefeuilles, Caprifoliaceae, originaire du Mexique. Poussant à 4 m (13 pi) de haut et large, c'est un arbuste semi-persistant ou à feuilles persistantes avec des feuilles ovales brillantes et des grappes de fleurs cerises tubulaires de 5 cm (2,0 po) de long. Bien que rustique jusqu'à -10 ° C (14 ° F), il préfère un endroit abrité, par exemple contre un mur de pierre exposé au sud.
Linnaea × grandiflora: Linnaea × grandiflora , synonyme Abelia × grandiflora , est une espèce hybride de plante à fleurs de la famille des chèvrefeuilles Caprifoliaceae, élevée par hybridation de L. chinensis avec L. uniflora .
Linnaea chinensis: Linnaea chinensis , synonymes Abelia chinensis et Abelia rupestris , est une espèce de plante à fleurs de la famille des chèvrefeuilles Caprifoliaceae. Il a été décrit par Robert Brown en 1818 et transféré au genre Linnaea en 1872, bien que ce mouvement n'ait pas été largement accepté avant 2013. La plante habite la Chine, Taiwan et le Japon. C'est un arbuste caduc compact avec des tiges rougeâtres et de petites feuilles brillantes qui deviennent brun rougeâtre avant l'automne. C'est l'une des espèces les plus résistantes au froid du genre.
Linnaea floribunda: Linnaea floribunda est une espèce de plante à fleurs de la famille des chèvrefeuilles, Caprifoliaceae, originaire du Mexique. Poussant à 4 m (13 pi) de haut et large, c'est un arbuste semi-persistant ou à feuilles persistantes avec des feuilles ovales brillantes et des grappes de fleurs cerises tubulaires de 5 cm (2,0 po) de long. Bien que rustique jusqu'à -10 ° C (14 ° F), il préfère un endroit abrité, par exemple contre un mur de pierre exposé au sud.
Linnaea chinensis: Linnaea chinensis , synonymes Abelia chinensis et Abelia rupestris , est une espèce de plante à fleurs de la famille des chèvrefeuilles Caprifoliaceae. Il a été décrit par Robert Brown en 1818 et transféré au genre Linnaea en 1872, bien que ce mouvement n'ait pas été largement accepté avant 2013. La plante habite la Chine, Taiwan et le Japon. C'est un arbuste caduc compact avec des tiges rougeâtres et de petites feuilles brillantes qui deviennent brun rougeâtre avant l'automne. C'est l'une des espèces les plus résistantes au froid du genre.
Linnaea spathulata: Linnaea spathulata , synonyme Abelia spathulata , est une espèce de Linnaea de la famille des chèvrefeuilles (Caprifoliaceae). La plante est endémique de Corée et du Japon.
Linnaea chinensis: Linnaea chinensis , synonymes Abelia chinensis et Abelia rupestris , est une espèce de plante à fleurs de la famille des chèvrefeuilles Caprifoliaceae. Il a été décrit par Robert Brown en 1818 et transféré au genre Linnaea en 1872, bien que ce mouvement n'ait pas été largement accepté avant 2013. La plante habite la Chine, Taiwan et le Japon. C'est un arbuste caduc compact avec des tiges rougeâtres et de petites feuilles brillantes qui deviennent brun rougeâtre avant l'automne. C'est l'une des espèces les plus résistantes au froid du genre.
Linnaea parvifolia: Linnaea parvifolia , synonyme Abelia schumannii , est une espèce de plante à fleurs de la famille des Caprifoliacées, originaire du centre de la Chine. C'est un arbuste semi-persistant atteignant 2 m (7 pi) de hauteur par 3 m (10 pi) de largeur. Des fleurs roses avec des calices rouges sont produites à la fin de l'été et à l'automne.
Linnaea parvifolia: Linnaea parvifolia , synonyme Abelia schumannii , est une espèce de plante à fleurs de la famille des Caprifoliacées, originaire du centre de la Chine. C'est un arbuste semi-persistant atteignant 2 m (7 pi) de hauteur par 3 m (10 pi) de largeur. Des fleurs roses avec des calices rouges sont produites à la fin de l'été et à l'automne.
Zabelia tyaihyonii: Zabelia tyaihyonii , synonyme Abelia mosanensis , connu sous le nom d' abelia parfumé , est une espèce d'arbuste à feuilles caduques de la famille des chèvrefeuilles Caprifoliaceae. Poussant jusqu'à 2 mètres de haut et de large, il est plus résistant que de nombreuses espèces apparentées, survivant à des températures aussi basses que -20 ° C (-4 ° F). Les fleurs tubulaires sont blanc rosé et très parfumées, apparaissant à la fin du printemps. Les feuilles vertes brillantes deviennent rouges en automne avant de tomber.
Linnaea parvifolia: Linnaea parvifolia , synonyme Abelia schumannii , est une espèce de plante à fleurs de la famille des Caprifoliacées, originaire du centre de la Chine. C'est un arbuste semi-persistant atteignant 2 m (7 pi) de hauteur par 3 m (10 pi) de largeur. Des fleurs roses avec des calices rouges sont produites à la fin de l'été et à l'automne.
Linnaea parvifolia: Linnaea parvifolia , synonyme Abelia schumannii , est une espèce de plante à fleurs de la famille des Caprifoliacées, originaire du centre de la Chine. C'est un arbuste semi-persistant atteignant 2 m (7 pi) de hauteur par 3 m (10 pi) de largeur. Des fleurs roses avec des calices rouges sont produites à la fin de l'été et à l'automne.
Linnaea chinensis: Linnaea chinensis , synonymes Abelia chinensis et Abelia rupestris , est une espèce de plante à fleurs de la famille des chèvrefeuilles Caprifoliaceae. Il a été décrit par Robert Brown en 1818 et transféré au genre Linnaea en 1872, bien que ce mouvement n'ait pas été largement accepté avant 2013. La plante habite la Chine, Taiwan et le Japon. C'est un arbuste caduc compact avec des tiges rougeâtres et de petites feuilles brillantes qui deviennent brun rougeâtre avant l'automne. C'est l'une des espèces les plus résistantes au froid du genre.
Linnaea spathulata: Linnaea spathulata , synonyme Abelia spathulata , est une espèce de Linnaea de la famille des chèvrefeuilles (Caprifoliaceae). La plante est endémique de Corée et du Japon.
Linnaea parvifolia: Linnaea parvifolia , synonyme Abelia schumannii , est une espèce de plante à fleurs de la famille des Caprifoliacées, originaire du centre de la Chine. C'est un arbuste semi-persistant atteignant 2 m (7 pi) de hauteur par 3 m (10 pi) de largeur. Des fleurs roses avec des calices rouges sont produites à la fin de l'été et à l'automne.
Linnaea parvifolia: Linnaea parvifolia , synonyme Abelia schumannii , est une espèce de plante à fleurs de la famille des Caprifoliacées, originaire du centre de la Chine. C'est un arbuste semi-persistant atteignant 2 m (7 pi) de hauteur par 3 m (10 pi) de largeur. Des fleurs roses avec des calices rouges sont produites à la fin de l'été et à l'automne.
Linnaea spathulata: Linnaea spathulata , synonyme Abelia spathulata , est une espèce de Linnaea de la famille des chèvrefeuilles (Caprifoliaceae). La plante est endémique de Corée et du Japon.
Linnaea floribunda: Linnaea floribunda est une espèce de plante à fleurs de la famille des chèvrefeuilles, Caprifoliaceae, originaire du Mexique. Poussant à 4 m (13 pi) de haut et large, c'est un arbuste semi-persistant ou à feuilles persistantes avec des feuilles ovales brillantes et des grappes de fleurs cerises tubulaires de 5 cm (2,0 po) de long. Bien que rustique jusqu'à -10 ° C (14 ° F), il préfère un endroit abrité, par exemple contre un mur de pierre exposé au sud.
Linnaea parvifolia: Linnaea parvifolia , synonyme Abelia schumannii , est une espèce de plante à fleurs de la famille des Caprifoliacées, originaire du centre de la Chine. C'est un arbuste semi-persistant atteignant 2 m (7 pi) de hauteur par 3 m (10 pi) de largeur. Des fleurs roses avec des calices rouges sont produites à la fin de l'été et à l'automne.
Zabelia tyaihyonii: Zabelia tyaihyonii , synonyme Abelia mosanensis , connu sous le nom d' abelia parfumé , est une espèce d'arbuste à feuilles caduques de la famille des chèvrefeuilles Caprifoliaceae. Poussant jusqu'à 2 mètres de haut et de large, il est plus résistant que de nombreuses espèces apparentées, survivant à des températures aussi basses que -20 ° C (-4 ° F). Les fleurs tubulaires sont blanc rosé et très parfumées, apparaissant à la fin du printemps. Les feuilles vertes brillantes deviennent rouges en automne avant de tomber.
Linnaea parvifolia: Linnaea parvifolia , synonyme Abelia schumannii , est une espèce de plante à fleurs de la famille des Caprifoliacées, originaire du centre de la Chine. C'est un arbuste semi-persistant atteignant 2 m (7 pi) de hauteur par 3 m (10 pi) de largeur. Des fleurs roses avec des calices rouges sont produites à la fin de l'été et à l'automne.
Linnaea × grandiflora: Linnaea × grandiflora , synonyme Abelia × grandiflora , est une espèce hybride de plante à fleurs de la famille des chèvrefeuilles Caprifoliaceae, élevée par hybridation de L. chinensis avec L. uniflora .
Linnaea × grandiflora: Linnaea × grandiflora , synonyme Abelia × grandiflora , est une espèce hybride de plante à fleurs de la famille des chèvrefeuilles Caprifoliaceae, élevée par hybridation de L. chinensis avec L. uniflora .
Linnaea × grandiflora: Linnaea × grandiflora , synonyme Abelia × grandiflora , est une espèce hybride de plante à fleurs de la famille des chèvrefeuilles Caprifoliaceae, élevée par hybridation de L. chinensis avec L. uniflora .
Abelian: Abelian peut faire référence à:
Théorèmes abélien et taubérien: En mathématiques, les théorèmes abélien et taubérien sont des théorèmes donnant des conditions pour que deux méthodes de sommation de séries divergentes donnent le même résultat, du nom de Niels Henrik Abel et Alfred Tauber. Les exemples originaux sont le théorème d'Abel montrant que si une série converge vers une certaine limite alors sa somme d'Abel est la même limite, et le théorème de Tauber montrant que si la somme d'Abel d'une série existe et que les coefficients sont suffisamment petits alors la série converge vers l'Abel somme. Des théorèmes abéliens et taubériens plus généraux donnent des résultats similaires pour des méthodes de sommation plus générales.
Abelian: Abelian peut faire référence à:
Abelian: Abelian peut faire référence à:
Groupe Abelian 2: En mathématiques, un groupe 2 abélien est un analogue dimensionnel supérieur d'un groupe abélien, au sens de l'algèbre supérieure, qui a été introduit à l'origine par Alexander Grothendieck lors de l'étude des structures abstraites entourant les variétés abéliennes et les groupes picards. Plus concrètement, ils sont donnés par des groupoïdes qui ont un bifoncteur qui agit formellement comme l'addition d'un groupe abélien. À savoir, le bifoncteur a une notion de commutativité, d'associativité et de structure identitaire. Bien que cela semble être une structure assez élevée et abstraite, il existe plusieurs exemples de 2-groupes abéliens. En fait, certains d'entre eux fournissent des prototypes pour des exemples plus complexes de structures algébriques supérieures, telles que les n-groupes abéliens.
Catégorie abélienne: En mathématiques, une catégorie abélienne est une catégorie dans laquelle des morphismes et des objets peuvent être ajoutés et dans laquelle des noyaux et des noyaux existent et ont des propriétés souhaitables. L'exemple prototypique motivant d'une catégorie abélienne est la catégorie des groupes abéliens, Ab . La théorie est née dans un effort d'unifier plusieurs théories de cohomologie par Alexander Grothendieck et indépendamment dans les travaux légèrement antérieurs de David Buchsbaum. Les catégories abéliennes sont des catégories très stables ; par exemple, ils sont réguliers et ils satisfont le lemme du serpent. La classe des catégories abéliennes est fermée sous plusieurs constructions catégoriques, par exemple, la catégorie des complexes de chaînes d'une catégorie abélienne, ou la catégorie des foncteurs d'une petite catégorie à une catégorie abélienne sont également abéliennes. Ces propriétés de stabilité les rendent inévitables en algèbre homologique et au-delà; la théorie a des applications majeures dans la géométrie algébrique, la cohomologie et la théorie des catégories pures. Les catégories abéliennes portent le nom de Niels Henrik Abel.
Différentiel du premier type: En mathématiques, le différentiel du premier type est un terme traditionnel utilisé dans les théories des surfaces de Riemann et des courbes algébriques, pour les formes 1 différentielles régulières partout. Etant donné une variété complexe M , une différentielle du premier type ω est donc la même chose qu'une forme 1 qui est partout holomorphe; sur une variété algébrique V non singulière ce serait une section globale du faisceau cohérent Ω 1 des différentiels de Kähler. Dans les deux cas, la définition a ses origines dans la théorie des intégrales abéliennes.
Extension abélienne: En algèbre abstraite, une extension abélienne est une extension galoisienne dont le groupe de Galois est abélien. Lorsque le groupe de Galois est également cyclique, l'extension est également appelée extension cyclique . Dans l'autre sens, une extension de Galois est dite solvable si son groupe de Galois est résoluble, c'est-à-dire si le groupe peut être décomposé en une série d'extensions normales d'un groupe abélien.
Variété abélienne: En mathématiques, en particulier en géométrie algébrique, en analyse complexe et en théorie algébrique des nombres, une variété abélienne est une variété algébrique projective qui est aussi un groupe algébrique, c'est-à-dire a une loi de groupe qui peut être définie par des fonctions régulières. Les variétés abéliennes font à la fois partie des objets les plus étudiés en géométrie algébrique et outils indispensables pour de nombreuses recherches sur d'autres sujets en géométrie algébrique et en théorie des nombres.
Groupe abélien: En mathématiques, un groupe abélien , également appelé groupe commutatif , est un groupe dans lequel le résultat de l'application de l'opération de groupe à deux éléments de groupe ne dépend pas de l'ordre dans lequel ils sont écrits. Autrement dit, l'opération de groupe est commutative. Avec l'addition comme opération, les entiers et les nombres réels forment des groupes abéliens, et le concept de groupe abélien peut être considéré comme une généralisation de ces exemples. Les groupes abéliens portent le nom du mathématicien du début du XIXe siècle Niels Henrik Abel.
Mécanisme de Higgs: Dans le modèle standard de physique des particules, le mécanisme de Higgs est essentiel pour expliquer le mécanisme de génération de la propriété «masse» pour les bosons de jauge. Sans le mécanisme de Higgs, tous les bosons (l'une des deux classes de particules, l'autre étant des fermions) seraient considérés comme sans masse, mais les mesures montrent que les bosons W + , W - et Z 0 ont en fait des masses relativement importantes d'environ 80 GeV. / c 2 . Le champ Higgs résout cette énigme. La description la plus simple du mécanisme ajoute un champ quantique (le champ de Higgs) qui imprègne tout l'espace du modèle standard. En dessous d'une température extrêmement élevée, le champ provoque une rupture spontanée de symétrie lors des interactions. La rupture de la symétrie déclenche le mécanisme de Higgs, ce qui fait que les bosons avec lesquels il interagit ont une masse. Dans le modèle standard, l'expression «mécanisme de Higgs» se réfère spécifiquement à la génération de masses pour les bosons de jauge faible W ± et Z par rupture de symétrie électrofaible. Le Grand collisionneur de hadrons du CERN a annoncé des résultats cohérents avec la particule de Higgs le 14 mars 2013, ce qui rend extrêmement probable l'existence du champ, ou un champ similaire, et explique comment le mécanisme de Higgs se déroule dans la nature.
Mécanisme de Higgs: Dans le modèle standard de physique des particules, le mécanisme de Higgs est essentiel pour expliquer le mécanisme de génération de la propriété «masse» pour les bosons de jauge. Sans le mécanisme de Higgs, tous les bosons (l'une des deux classes de particules, l'autre étant des fermions) seraient considérés comme sans masse, mais les mesures montrent que les bosons W + , W - et Z 0 ont en fait des masses relativement importantes d'environ 80 GeV. / c 2 . Le champ Higgs résout cette énigme. La description la plus simple du mécanisme ajoute un champ quantique (le champ de Higgs) qui imprègne tout l'espace du modèle standard. En dessous d'une température extrêmement élevée, le champ provoque une rupture spontanée de symétrie lors des interactions. La rupture de la symétrie déclenche le mécanisme de Higgs, ce qui fait que les bosons avec lesquels il interagit ont une masse. Dans le modèle standard, l'expression «mécanisme de Higgs» se réfère spécifiquement à la génération de masses pour les bosons de jauge faible W ± et Z par rupture de symétrie électrofaible. Le Grand collisionneur de hadrons du CERN a annoncé des résultats cohérents avec la particule de Higgs le 14 mars 2013, ce qui rend extrêmement probable l'existence du champ, ou un champ similaire, et explique comment le mécanisme de Higgs se déroule dans la nature.
Intégrale abélienne: En mathématiques, une intégrale abélienne , du nom du mathématicien norvégien Niels Henrik Abel, est une intégrale dans le plan complexe de la forme
Algèbre de Lie: En mathématiques, une algèbre de Lie est un espace vectoriel avec une opération appelée le crochet de Lie , une carte bilinéaire alternée , qui satisfait l'identité Jacobi. L'espace vectoriel avec cette opération est une algèbre non associative, ce qui signifie que la parenthèse de Lie n'est pas nécessairement associative.
Groupe de Lie abélien: En géométrie, un groupe de Lie abélien est un groupe de Lie qui est un groupe abélien.
Polynômes d'Abel: Les polynômes d'Abel en mathématiques forment une séquence polynomiale dont le n ème terme est de la forme
Théorèmes abélien et taubérien: En mathématiques, les théorèmes abélien et taubérien sont des théorèmes donnant des conditions pour que deux méthodes de sommation de séries divergentes donnent le même résultat, du nom de Niels Henrik Abel et Alfred Tauber. Les exemples originaux sont le théorème d'Abel montrant que si une série converge vers une certaine limite alors sa somme d'Abel est la même limite, et le théorème de Tauber montrant que si la somme d'Abel d'une série existe et que les coefficients sont suffisamment petits alors la série converge vers l'Abel somme. Des théorèmes abéliens et taubériens plus généraux donnent des résultats similaires pour des méthodes de sommation plus générales.
Variété abélienne: En mathématiques, en particulier en géométrie algébrique, en analyse complexe et en théorie algébrique des nombres, une variété abélienne est une variété algébrique projective qui est également un groupe algébrique, c'est-à-dire a une loi de groupe qui peut être définie par des fonctions régulières. Les variétés abéliennes font à la fois partie des objets les plus étudiés en géométrie algébrique et des outils indispensables pour de nombreuses recherches sur d'autres sujets en géométrie algébrique et en théorie des nombres.
Algèbre associative: En mathématiques, une algèbre associative est une structure algébrique avec des opérations compatibles d'addition, de multiplication et de multiplication scalaire par éléments dans certains domaines. Les opérations d'addition et de multiplication donnent ensemble à A la structure d'un anneau; les opérations d'addition et de multiplication scalaire donnent ensemble à A la structure d'un espace vectoriel sur K. Dans cet article, nous utiliserons également le terme K -algèbre pour désigner une algèbre associative sur le corps K. Un premier exemple standard d'algèbre K est un anneau de matrices carrées sur un champ K , avec la multiplication matricielle habituelle.
Théorèmes abélien et taubérien: En mathématiques, les théorèmes abélien et taubérien sont des théorèmes donnant des conditions pour que deux méthodes de sommation de séries divergentes donnent le même résultat, du nom de Niels Henrik Abel et Alfred Tauber. Les exemples originaux sont le théorème d'Abel montrant que si une série converge vers une certaine limite alors sa somme d'Abel est la même limite, et le théorème de Tauber montrant que si la somme d'Abel d'une série existe et que les coefficients sont suffisamment petits alors la série converge vers l'Abel somme. Des théorèmes abéliens et taubériens plus généraux donnent des résultats similaires pour des méthodes de sommation plus générales.
Théorèmes abélien et taubérien: En mathématiques, les théorèmes abélien et taubérien sont des théorèmes donnant des conditions pour que deux méthodes de sommation de séries divergentes donnent le même résultat, du nom de Niels Henrik Abel et Alfred Tauber. Les exemples originaux sont le théorème d'Abel montrant que si une série converge vers une certaine limite alors sa somme d'Abel est la même limite, et le théorème de Tauber montrant que si la somme d'Abel d'une série existe et que les coefficients sont suffisamment petits alors la série converge vers l'Abel somme. Des théorèmes abéliens et taubériens plus généraux donnent des résultats similaires pour des méthodes de sommation plus générales.
Catégorie abélienne: En mathématiques, une catégorie abélienne est une catégorie dans laquelle des morphismes et des objets peuvent être ajoutés et dans laquelle des noyaux et des noyaux existent et ont des propriétés souhaitables. L'exemple prototypique motivant d'une catégorie abélienne est la catégorie des groupes abéliens, Ab . La théorie est née dans un effort d'unifier plusieurs théories de cohomologie par Alexander Grothendieck et indépendamment dans les travaux légèrement antérieurs de David Buchsbaum. Les catégories abéliennes sont des catégories très stables ; par exemple, ils sont réguliers et ils satisfont le lemme du serpent. La classe des catégories abéliennes est fermée sous plusieurs constructions catégoriques, par exemple, la catégorie des complexes de chaînes d'une catégorie abélienne, ou la catégorie des foncteurs d'une petite catégorie à une catégorie abélienne sont également abéliennes. Ces propriétés de stabilité les rendent inévitables en algèbre homologique et au-delà; la théorie a des applications majeures dans la géométrie algébrique, la cohomologie et la théorie des catégories pures. Les catégories abéliennes portent le nom de Niels Henrik Abel.
Catégorie abélienne: En mathématiques, une catégorie abélienne est une catégorie dans laquelle des morphismes et des objets peuvent être ajoutés et dans laquelle des noyaux et des noyaux existent et ont des propriétés souhaitables. L'exemple prototypique motivant d'une catégorie abélienne est la catégorie des groupes abéliens, Ab . La théorie est née dans un effort d'unifier plusieurs théories de cohomologie par Alexander Grothendieck et indépendamment dans les travaux légèrement antérieurs de David Buchsbaum. Les catégories abéliennes sont des catégories très stables ; par exemple, ils sont réguliers et ils satisfont le lemme du serpent. La classe des catégories abéliennes est fermée sous plusieurs constructions catégoriques, par exemple, la catégorie des complexes de chaînes d'une catégorie abélienne, ou la catégorie des foncteurs d'une petite catégorie à une catégorie abélienne sont également abéliennes. Ces propriétés de stabilité les rendent inévitables en algèbre homologique et au-delà; la théorie a des applications majeures dans la géométrie algébrique, la cohomologie et la théorie des catégories pures. Les catégories abéliennes portent le nom de Niels Henrik Abel.
Fonction de complexité: En informatique, la fonction de complexité d'une chaîne, une séquence finie ou infinie de lettres d'un alphabet, est la fonction qui compte le nombre de facteurs distincts de cette chaîne. Plus généralement, la fonction de complexité d'une langue, un ensemble de mots finis sur un alphabet, compte le nombre de mots distincts de longueur donnée.
Groupe de couverture: En mathématiques, un groupe de recouvrement d'un groupe topologique H est un espace de recouvrement G de H tel que G est un groupe topologique et la carte de recouvrement p : G → H est un homomorphisme de groupe continu. La carte p est appelée l' homomorphisme couvrant . Un cas fréquemment rencontré est un groupe à double couverture , une double couverture topologique dans laquelle H a l'indice 2 dans G ; les exemples incluent les groupes de spin, les groupes de broches et les groupes métaplectiques.
Différentiel du premier type: En mathématiques, le différentiel du premier type est un terme traditionnel utilisé dans les théories des surfaces de Riemann et des courbes algébriques, pour les formes 1 différentielles régulières partout. Etant donné une variété complexe M , une différentielle du premier type ω est donc la même chose qu'une forme 1 qui est partout holomorphe; sur une variété algébrique V non singulière ce serait une section globale du faisceau cohérent Ω 1 des différentiels de Kähler. Dans les deux cas, la définition a ses origines dans la théorie des intégrales abéliennes.
Extension abélienne: En algèbre abstraite, une extension abélienne est une extension galoisienne dont le groupe de Galois est abélien. Lorsque le groupe de Galois est également cyclique, l'extension est également appelée extension cyclique . Dans l'autre sens, une extension de Galois est dite solvable si son groupe de Galois est résoluble, c'est-à-dire si le groupe peut être décomposé en une série d'extensions normales d'un groupe abélien.
Extension abélienne: En algèbre abstraite, une extension abélienne est une extension galoisienne dont le groupe de Galois est abélien. Lorsque le groupe de Galois est également cyclique, l'extension est également appelée extension cyclique . Dans l'autre sens, une extension de Galois est dite solvable si son groupe de Galois est résoluble, c'est-à-dire si le groupe peut être décomposé en une série d'extensions normales d'un groupe abélien.
Variété abélienne: En mathématiques, en particulier en géométrie algébrique, en analyse complexe et en théorie algébrique des nombres, une variété abélienne est une variété algébrique projective qui est aussi un groupe algébrique, c'est-à-dire a une loi de groupe qui peut être définie par des fonctions régulières. Les variétés abéliennes font à la fois partie des objets les plus étudiés en géométrie algébrique et outils indispensables pour de nombreuses recherches sur d'autres sujets en géométrie algébrique et en théorie des nombres.
Théorie de la jauge: En physique, une théorie de jauge est un type de théorie des champs dans laquelle le lagrangien ne change pas sous les transformations locales de certains groupes de Lie.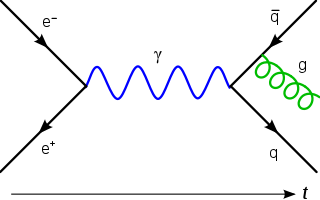
Blague mathématique: Une blague mathématique est une forme d'humour qui s'appuie sur des aspects mathématiques ou sur un stéréotype de mathématiciens. L'humour peut provenir d'un jeu de mots, ou d'un double sens d'un terme mathématique, ou d'une incompréhension d'un profane d'un concept mathématique. Le mathématicien et auteur John Allen Paulos, dans son livre Mathematics and Humor, a décrit plusieurs façons dont les mathématiques, généralement considérées comme une activité sèche et formelle, se chevauchent avec l'humour, une activité lâche et irrévérencieuse: les deux sont des formes de «jeu intellectuel»; les deux ont «logique, modèle, règles, structure»; et les deux sont «économiques et explicites».
Groupe abélien: En mathématiques, un groupe abélien , également appelé groupe commutatif , est un groupe dans lequel le résultat de l'application de l'opération de groupe à deux éléments de groupe ne dépend pas de l'ordre dans lequel ils sont écrits. Autrement dit, l'opération de groupe est commutative. Avec l'addition comme opération, les entiers et les nombres réels forment des groupes abéliens, et le concept de groupe abélien peut être considéré comme une généralisation de ces exemples. Les groupes abéliens portent le nom du mathématicien du début du XIXe siècle Niels Henrik Abel.
Groupe abélien: En mathématiques, un groupe abélien , également appelé groupe commutatif , est un groupe dans lequel le résultat de l'application de l'opération de groupe à deux éléments de groupe ne dépend pas de l'ordre dans lequel ils sont écrits. Autrement dit, l'opération de groupe est commutative. Avec l'addition comme opération, les entiers et les nombres réels forment des groupes abéliens, et le concept de groupe abélien peut être considéré comme une généralisation de ces exemples. Les groupes abéliens portent le nom du mathématicien du début du XIXe siècle Niels Henrik Abel.
Intégrale abélienne: En mathématiques, une intégrale abélienne , du nom du mathématicien norvégien Niels Henrik Abel, est une intégrale dans le plan complexe de la forme
Formule de localisation pour la cohomologie équivariante: En géométrie différentielle, la formule de localisation indique: pour une forme différentielle équivariante fermée équivariante sur un orbifold M avec une action de tore et pour une dans l'algèbre de Lie du tore T ,
Série divergente: En mathématiques, une série divergente est une série infinie qui n'est pas convergente, ce qui signifie que la suite infinie des sommes partielles de la série n'a pas de limite finie.
Monoïde: Dans l'algèbre abstraite, une branche des mathématiques, un monoïde est un ensemble équipé d'une opération binaire associative et d'un élément d'identité.
Théorie des champs de classe: En mathématiques, la théorie des champs de classe est la branche de la théorie algébrique des nombres concernée par les extensions abéliennes des champs de nombres, les champs globaux de caractéristique positive et les champs locaux. La théorie a ses origines dans la preuve de la réciprocité quadratique par Gauss à la fin du 18ème siècle. Ces idées ont été développées au cours du siècle suivant, donnant lieu à un ensemble de conjectures de Hilbert qui ont ensuite été prouvées par Takagi et Artin. Ces conjectures et leurs preuves constituent le corps principal de la théorie des champs de classe.
Idempotent (théorie des anneaux): Dans la théorie des anneaux, un élément idempotent , ou simplement un idempotent , d'un anneau est un élément a tel que a 2 = a . Autrement dit, l'élément est idempotent sous la multiplication de l'anneau. Inductivement alors, on peut aussi conclure que a = a 2 = a 3 = a 4 = ... = a n pour tout entier positif n . Par exemple, un élément idempotent d'un anneau de matrice est précisément une matrice idempotente.
Modèle de tas de sable abélien: Le modèle de tas de sable abélien , également connu sous le nom de modèle de Bak – Tang – Wiesenfeld , a été le premier exemple découvert d'un système dynamique affichant une criticité auto-organisée. Il a été introduit par Per Bak, Chao Tang et Kurt Wiesenfeld dans un article de 1987.
Modèle de tas de sable abélien: Le modèle de tas de sable abélien , également connu sous le nom de modèle de Bak – Tang – Wiesenfeld , a été le premier exemple découvert d'un système dynamique affichant une criticité auto-organisée. Il a été introduit par Per Bak, Chao Tang et Kurt Wiesenfeld dans un article de 1987.
Variété abélienne: En mathématiques, en particulier en géométrie algébrique, en analyse complexe et en théorie algébrique des nombres, une variété abélienne est une variété algébrique projective qui est aussi un groupe algébrique, c'est-à-dire a une loi de groupe qui peut être définie par des fonctions régulières. Les variétés abéliennes font à la fois partie des objets les plus étudiés en géométrie algébrique et outils indispensables pour de nombreuses recherches sur d'autres sujets en géométrie algébrique et en théorie des nombres.
Semi-groupe: En mathématiques, un semigroupe est une structure algébrique constituée d'un ensemble avec une opération binaire associative.
Gerbe de modules: En mathématiques, un faisceau de O -modules ou simplement un O -module sur un espace annelé est un faisceau F tel que, pour tout sous-ensemble ouvert U de X , F ( U ) est un O ( U ) -module et les cartes de restriction F ( U ) → F ( V ) sont compatibles avec les cartes de restriction O ( U ) → O ( V ): la restriction de fs est la restriction de f fois celle de s pour tout f dans O ( U ) et s dans F ( U ).
Groupe abélien: En mathématiques, un groupe abélien , également appelé groupe commutatif , est un groupe dans lequel le résultat de l'application de l'opération de groupe à deux éléments de groupe ne dépend pas de l'ordre dans lequel ils sont écrits. Autrement dit, l'opération de groupe est commutative. Avec l'addition comme opération, les entiers et les nombres réels forment des groupes abéliens, et le concept de groupe abélien peut être considéré comme une généralisation de ces exemples. Les groupes abéliens portent le nom du mathématicien du début du XIXe siècle Niels Henrik Abel.
Théorème d'Abel: En mathématiques, le théorème d' Abel pour les séries de puissance relie une limite d'une série de puissance à la somme de ses coefficients. Il porte le nom du mathématicien norvégien Niels Henrik Abel.
Surface abélienne: En mathématiques, une surface abélienne est une variété abélienne à 2 dimensions.
Théorèmes abélien et taubérien: En mathématiques, les théorèmes abélien et taubérien sont des théorèmes donnant des conditions pour que deux méthodes de sommation de séries divergentes donnent le même résultat, du nom de Niels Henrik Abel et Alfred Tauber. Les exemples originaux sont le théorème d'Abel montrant que si une série converge vers une certaine limite alors sa somme d'Abel est la même limite, et le théorème de Tauber montrant que si la somme d'Abel d'une série existe et que les coefficients sont suffisamment petits alors la série converge vers l'Abel somme. Des théorèmes abéliens et taubériens plus généraux donnent des résultats similaires pour des méthodes de sommation plus générales.
Variété abélienne: En mathématiques, en particulier en géométrie algébrique, en analyse complexe et en théorie algébrique des nombres, une variété abélienne est une variété algébrique projective qui est aussi un groupe algébrique, c'est-à-dire a une loi de groupe qui peut être définie par des fonctions régulières. Les variétés abéliennes font à la fois partie des objets les plus étudiés en géométrie algébrique et outils indispensables pour de nombreuses recherches sur d'autres sujets en géométrie algébrique et en théorie des nombres.
Variété abélienne: En mathématiques, en particulier en géométrie algébrique, en analyse complexe et en théorie algébrique des nombres, une variété abélienne est une variété algébrique projective qui est aussi un groupe algébrique, c'est-à-dire a une loi de groupe qui peut être définie par des fonctions régulières. Les variétés abéliennes font à la fois partie des objets les plus étudiés en géométrie algébrique et outils indispensables pour de nombreuses recherches sur d'autres sujets en géométrie algébrique et en théorie des nombres.
Localisation d'une catégorie: En mathématiques, la localisation d'une catégorie consiste à ajouter à une catégorie des morphismes inverses pour une collection de morphismes, les contraignant à devenir des isomorphismes. Ceci est formellement similaire au processus de localisation d'un anneau; il rend en général des objets isomorphes qui ne l'étaient pas auparavant. Dans la théorie de l'homotopie, par exemple, il existe de nombreux exemples de mappages qui sont inversibles jusqu'à l'homotopie; et donc de grandes classes d'espaces équivalents d'homotopie. Le calcul des fractions est un autre nom pour travailler dans une catégorie localisée.
Variété abélienne: En mathématiques, en particulier en géométrie algébrique, en analyse complexe et en théorie algébrique des nombres, une variété abélienne est une variété algébrique projective qui est aussi un groupe algébrique, c'est-à-dire a une loi de groupe qui peut être définie par des fonctions régulières. Les variétés abéliennes font à la fois partie des objets les plus étudiés en géométrie algébrique et outils indispensables pour de nombreuses recherches sur d'autres sujets en géométrie algébrique et en théorie des nombres.
Multiplication complexe de variétés abéliennes: En mathématiques, une variété abélienne A définie sur un corps K est dite de type CM si elle a un sous-rang commutatif assez grand dans son anneau d'endomorphisme End ( A ). La terminologie ici est tirée de la théorie de la multiplication complexe, qui a été développée pour les courbes elliptiques au XIXe siècle. L'une des réalisations majeures de la théorie algébrique des nombres et de la géométrie algébrique du XXe siècle a été de trouver les formulations correctes de la théorie correspondante pour les variétés abéliennes de dimension d > 1. Le problème se situe à un niveau d'abstraction plus profond, car il est beaucoup plus difficile. pour manipuler les fonctions analytiques de plusieurs variables complexes.
Algèbre d'Abelian von Neumann: En analyse fonctionnelle, une algèbre abélienne de von Neumann est une algèbre de von Neumann d'opérateurs sur un espace de Hilbert dans lequel tous les éléments commutent.
Algèbre d'Abelian von Neumann: En analyse fonctionnelle, une algèbre abélienne de von Neumann est une algèbre de von Neumann d'opérateurs sur un espace de Hilbert dans lequel tous les éléments commutent.
Sous-groupe de commutateurs: En mathématiques, plus précisément en algèbre abstraite, le sous -groupe de commutateurs ou sous -groupe dérivé d'un groupe est le sous-groupe généré par tous les commutateurs du groupe.
Sous-groupe de commutateurs: En mathématiques, plus précisément en algèbre abstraite, le sous -groupe de commutateurs ou sous -groupe dérivé d'un groupe est le sous-groupe généré par tous les commutateurs du groupe.
Abéliens: Les Abéliens étaient une secte chrétienne qui a vu le jour au 4ème siècle dans la campagne près d'Hippo Regius en Afrique du Nord pendant le règne d'Arcadius. Ils ont vécu dans la continence comme ils l'ont affirmé Abel. Ils étaient tenus de se marier, mais il leur était interdit de consommer le mariage. Chaque couple devait adopter deux enfants, un garçon et une fille. À la mort de leurs parents adoptifs, ces adoptés formaient alors un couple et adoptaient deux autres enfants. Puisqu'aucun enfant d'Abel n'est mentionné dans les Écritures, les Abéliens ont supposé qu'il n'en avait pas. Ce point de vue a été influencé par les perspectives gnostiques juives et manichéennes sur Abel qui reconnaissaient que, pendant qu'il était marié, il restait vierge. Le seul enregistrement de la secte est dans Augustin of Hippo's De Haereticis ch. 87 , où il écrit que le nom de la secte est probablement d'origine punique. Selon Augustin, la secte s'est éteinte en 428 lorsque ses derniers membres se sont convertis au catholicisme.